∵AD、BE是高
∴AD⊥BC,BE⊥AC
∴∠CAD+∠C=∠CBE+∠C=90°
∴∠CAD=∠CBE
∵∠ADC=∠BDH
∴△ADC∽△BDH
∴CD/HD=AD/BD
∴CD•BD=AD•HD
∵AD=BC
∴CD•BD=BC•HD
∴(FC+DF)(BF-DF)=BC•HD
∵F为BC的中点
∴BF=CF
∴(FC+DF)(FC-DF)=BC•HD
∴FC2-DF2=2FC•HD
移项得FC2-2FC•HD=DF2
两边同加上HD2得FC2-2FC•HD+HD2=HD2+DF2
即(FC-HD) 2=HD2+DF2
根据勾股定理有HD2+DF2=HF2
∴(FC-HD) 2=HF2
∴FC-HD=HF
∴FC=HF+HD











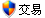

 此主题相关图片如下:
此主题相关图片如下: